Boyer–Moore 算法 是用来在字符串中搜索一个子字符串的算法,也简称 BM 算法。
问题
在长度为 n 的字符串 s 中搜索长度为 m 的子串 p 的位置。
本文以 ABCDABEABDCBCDDBBCDBACD 为主串 ,BCDBACD 为子串,作为用例。
算法过程
首先将两个字符串左对齐,对子串 p 进行 自右向左 的逐一比对。
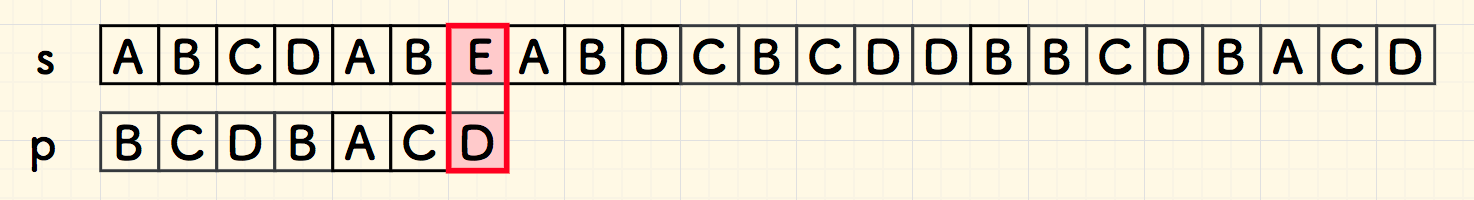
第一次比对,即在字符 E 失配。 由于 E 不在子串 p 中,因此,可以直接把整个子串右移到其右边。
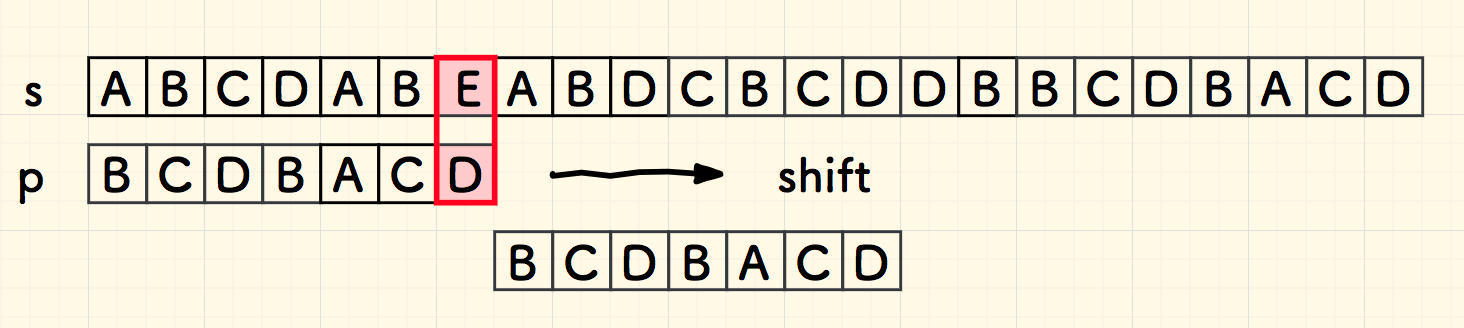
继续向前匹配,此时在下图中的红色部分失配。

但是,失配的 B 在子串 p 中,就在当前位置靠左一位的位置。 要想子串和主串在附近匹配成功,至少字符 B 要对的齐。 为了避免错过 B 的匹配,只能找到靠的最近的 B 对齐,也就是右移一位。
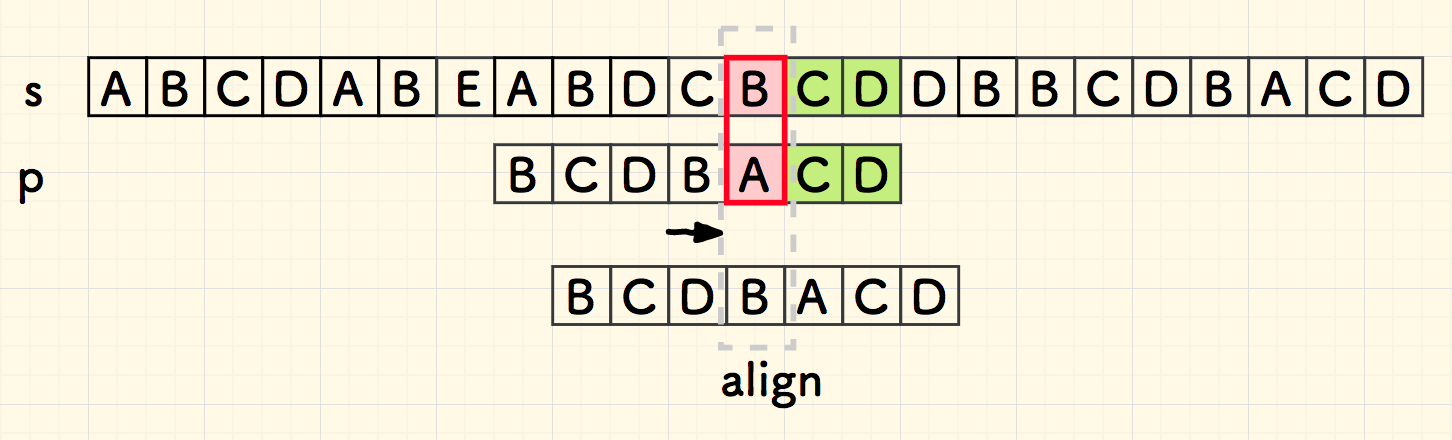
回到子串的尾部,自右向左,继续匹配,在下图中的红色部分失配。

沿用刚才上面的思路,失配的 D 也在子串中,右移 p ,让它们对齐
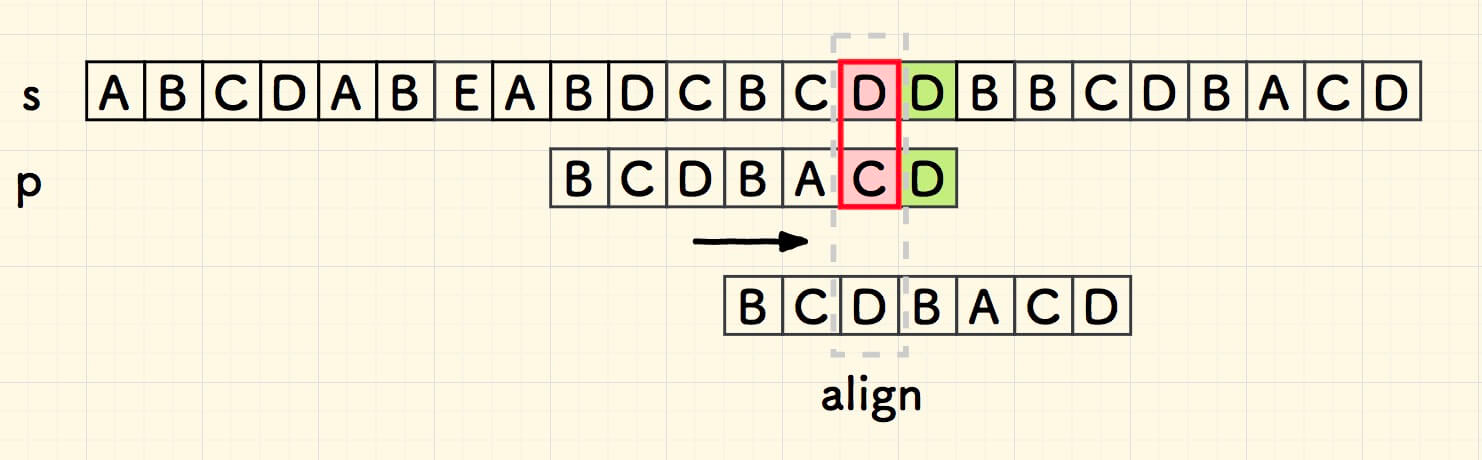
总结规律: 当失配的时候,右移子串,使得主串中失配的字符和子串中左边最近的相同字符对齐。如果不存在相同字符,就把整个子串右移到失配字符的右侧。
坏字符的办法
常把失配处主串中的字符叫做「坏字符」,每次右移,就要把 坏字符和子串中最近的坏字符对齐。
Boyer–Moore 算法和 KMP 算法 的思路类似,都是在失配处动脑筋,跳过无必要的比对,以加快搜索。
按这个思路,可以继续匹配下去,直到命中。
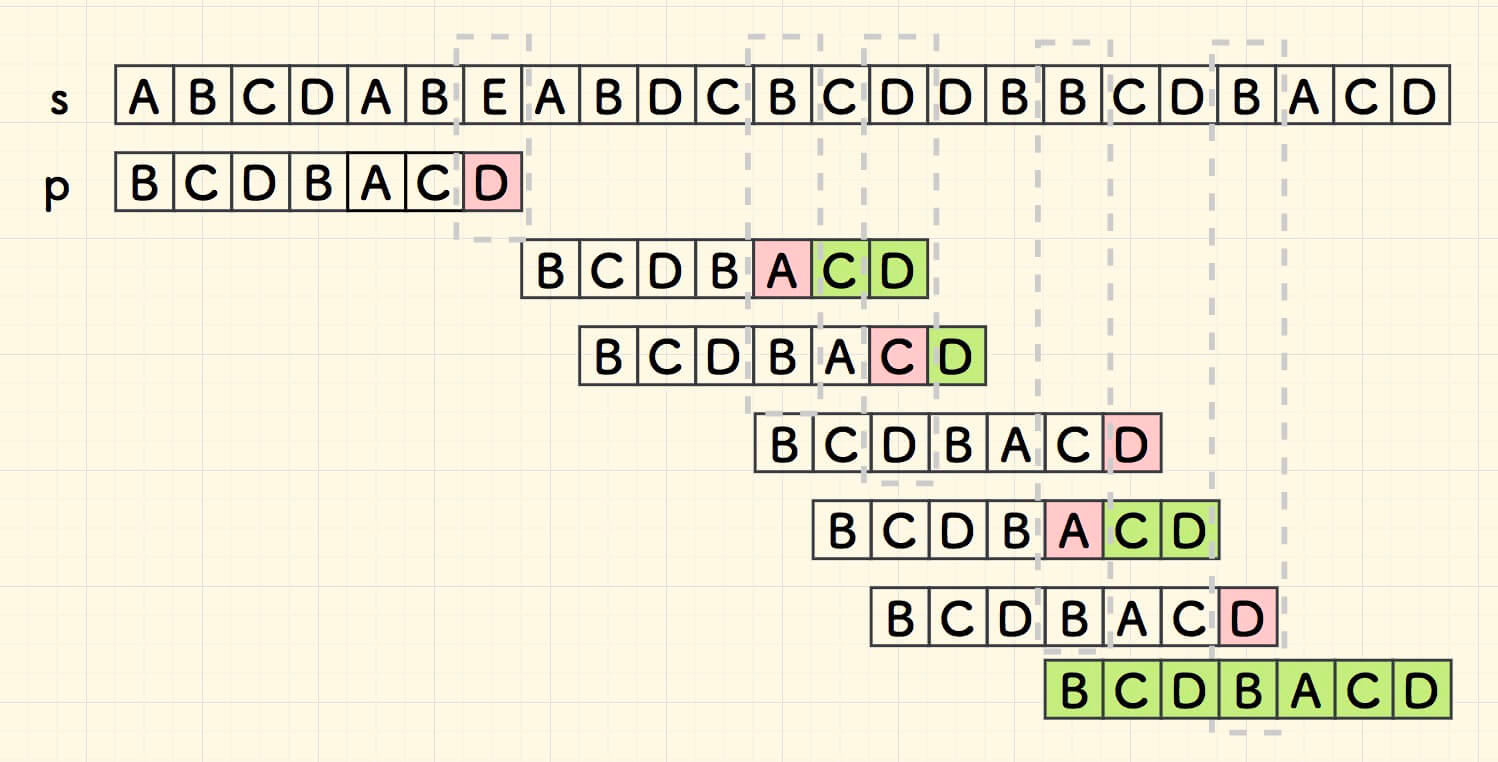
好后缀的办法
上面坏字符的办法,还不够快。
比如下面这次对齐:

此时,已知的信息是,主串中有已经匹配好的 CD ,它同时也是子串 p 的后缀,常叫做「好后缀」。
要想子串在附近和主串匹配成功,它们的共同子串 CD 就要对的齐,所以,把对齐坏字符的办法应用到好后缀上, 找到最近的好后缀进行右移对齐。
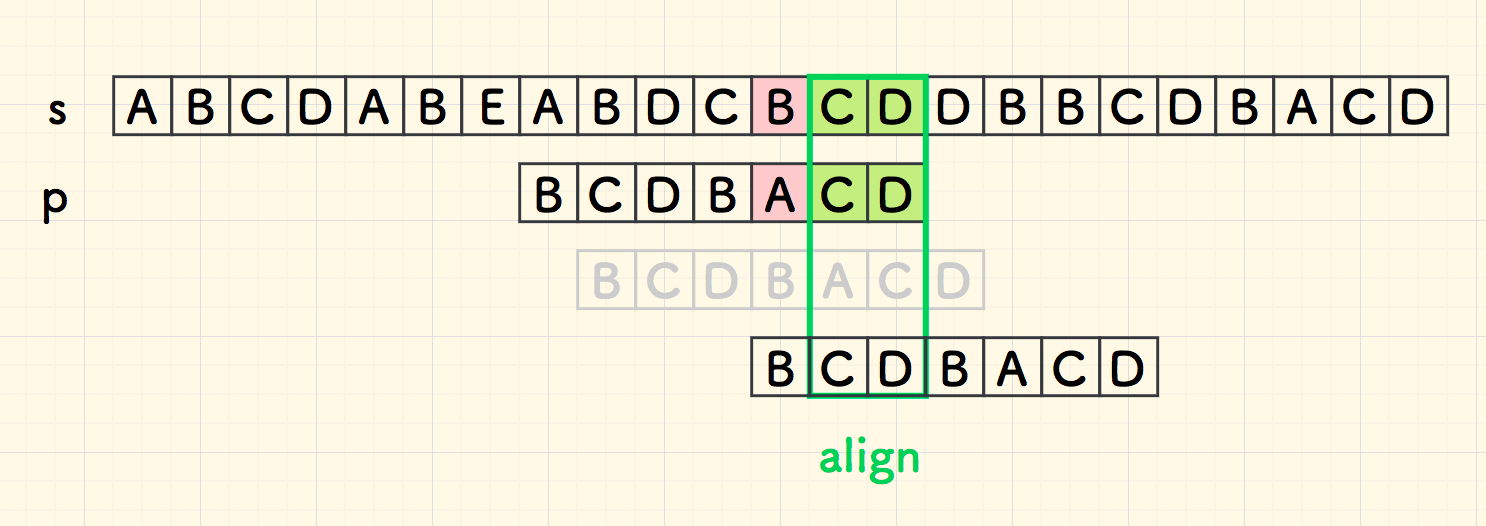
如此一来,右移的更多了些。
好后缀的办法就是, 失配时,右移子串,使得主串中的好后缀和子串中左边最近的重复串对齐 。 同样的,如果存在好后缀,而左边没有重复串时,那么直接把 p 右移到整个好后缀右边就好了。
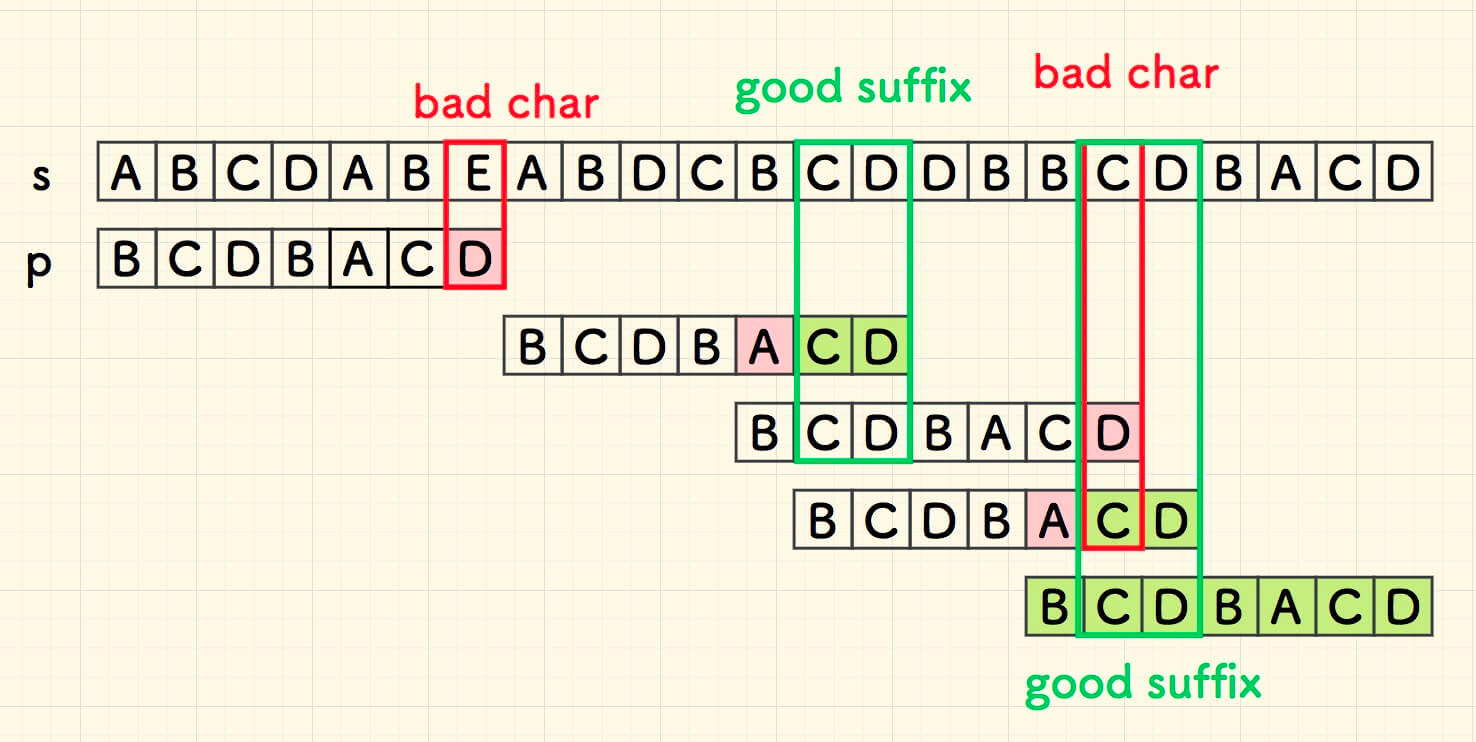
综合两个办法后,整个搜索过程优化为下面的样子,总体上比只用坏字符的办法,少了两步。